CF: Increasing Frequency
Algorithms

CF: Increasing Frequency

CF: Increasing Frequency Problem - 1082E - Codeforces 怎么说呢，DP的灵活度确实是比较高。当我看到 dp的tag时我已经在想怎么定状态想怎么转移什么的了。但是呢，其实这道题不用那个角度思考也可以，而且做题最重要的是找到数据的规律再总结出解决方案。

CF: Increasing Frequency

Problem - 1082E - Codeforces

怎么说呢，DP的灵活度确实是比较高。当我看到 dp的tag时我已经在想怎么定状态想怎么转移什么的了。但是呢，其实这道题不用那个角度思考也可以，而且做题最重要的是找到数据的规律再总结出解决方案。😂

回到这题，给定target C，问区间每个数+k一次，最多有多少数是C。OK，很直观​O(N^2)枚举两个端点是一个暴力的办法，但是超时😞

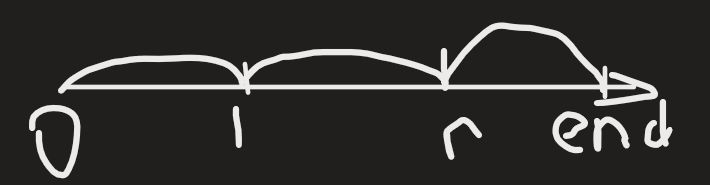
image-20240114023518243

现在，看看这个非常抽象的图😉，我们现在选了在0~end之间的l和r，形成3个区间。对于[0,l和(r,end]这两个区间，是不变的。

[0,l) & (r,end]

答案+上这两个区间中现有​c的个数，可以用前缀和保存。

[l,r]

我们的目标是从d->c.

这才是关键。在这个区间中，有​x个已经是​c的数值，还有​y个+完k会是​c的数值。可以这么考虑：从每一个不同的​a_i开始考虑，从小到大。​a_i作为区间内的​d，将其变为​c.

观察1:

如果是从​d开始的话，以​d结尾是最好的（避免在遇到下一个​d之前遇到​c）

这样子的话，我们可以定义一个类似于邻接表的东西：​ind[num][index]。​num就是从d=num开始，然后​index代表在这个​a里面​d出现的位置。

这个东西看起来像是​O(n^2)的，但因为vector是动态伸缩的，而要放的​index一共最多就​n个，所以这个东西是​O(n)不会炸。

观察2：

我们现在如果是对邻接表每一行的去看的话，按照暴力解法还是需要枚举两个端点，时间还是会爆。但是我们可以这么考虑：在​ind[num]中，​[0,.size()]是不是可以直接中间切开分治？

让​s=.size()，那么直接二分成​[0,s/2]和​[s/2,s]。然后合并就取正值的区间，然后加到一起-1，（要去掉那个多算的s/2这个点）。

思路2

来自洛谷CF1082E Increasing Frequency - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

image-20240116001453536

但是上述的思路和代码还是有点差距，这里我再补充一下。

现在已经得到式子​pre[a_i][r]-pre[c][r]-(pre[a_i][l-1]-pre[c][l-1])。这里说的“在遍历​i的时候动态存储”的意思其实是说在遍历的时候给他在数组里更新，之前保存最小的位置就是最优的​l-1，对应到​r=i的时候。所以​pre[a_i][r]和​pre[c][r]就是​pre[a_i][i]和​pre[c][i]。这样就给我们的二维问题压到了一维（非常优秀）。

/*
 * Created by: Chixiyu
 * Date: 2025-02-15
 */
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int bucket[N]; // bucket[i]=occurances of number i in array a
int dp[N];     // answer
int mn[N];
int ans = -1;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n, c;
    cin >> n >> c;
    vector<int> a(n);
    // init mn
    for (int i = 0; i <= n; i++) {
        mn[i] = INT_MAX;
    }
    // input
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    // start dp
    for (int i = 1; i <= n; i++) {
        // update minimum (pre[a[i]][l-1]-pre[c][l-1])
        mn[a[i]] = min(bucket[a[i]] - bucket[c], mn[a[i]]);
        bucket[a[i]]++;
        dp[i] = max(dp[i], bucket[a[i]] - bucket[c] - mn[a[i]]);
    }
    for (int i = 1; i <= n; i++) {
        ans = max(ans, dp[i] + bucket[c]);
    }
    cout << ans << endl;
    return 0;
}
Comment